✅ 깊이 우선 탐색(DFS, Depth-First Search)
트리 또는 그래프를 탐색하는 알고리즘으로, 시작점에서 출발하여 가능한 한 깊숙이 탐색해 나가는 방법이다. 이러한 방식으로 트리를 순회할 때, 전위 순회(Pre-Order)는 DFS 중에서도 가장 일반적인 방법 중 하나이며, 전위 순회 외에도 중위 순회(In-Order)나 후위 순회(Post-Order) 등도 DFS의 한 종류이다.
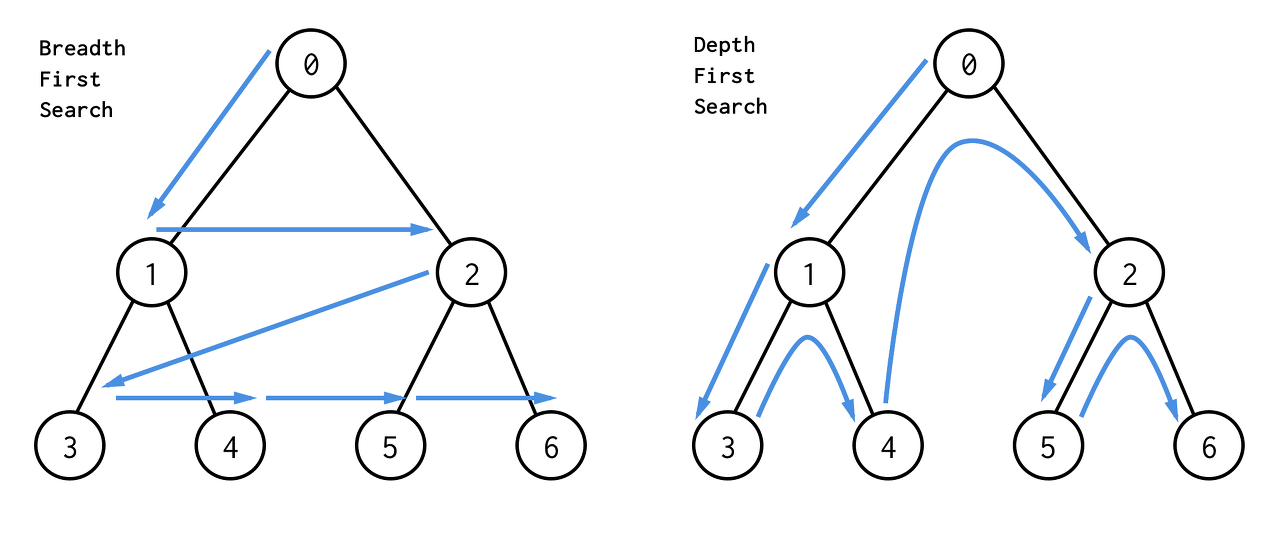
🤔 깊이 우선 탐색의 특징
- 스택이나 재귀 함수를 이용해서 구현 가능하다.
- 탐색 경로를 기억하지 않아, 특정한 경로를 찾는 문제에는 너비 우선 탐색(BFS)이 더 적합하다.
- 구현이 쉽고 속도가 빠르다.
- 한번 방문한 노드를 다시 방문하지 않는 것이 아니기에 무한 그래프에 빠질 위험이 있다. 이를 방지하기 위해 탐색 깊이를 제한하거나, 이미 방문한 노드를 따로 표시해 줘서 재방문하지 않도록 한다.
🟢 전위 순회(Pre-Order)
루트 노드를 가장 먼저 탐색하고, 그다음에 왼쪽 서브트리, 그다음에 오른쪽 서브트리를 탐색한다.
🟡 의사코드
- 방문했던 노드를 저장하는 변수를 만든다.
- current라 불리는 변수를 만들고, 트리의 루트를 저장해 준다. - 시작점
- node를 받는 헬퍼 함수를 작성한다.
- 방문한 값들을 저장하는 변수에 노드의 값을 push 한다.
- 만약 left를 가지고 있는 노드라면, 재귀 방식으로 헬퍼 함수를 다시 호출한다.
- 만약 right를 가지고 있는 노드라면, 재귀 방식으로 헬퍼 함수를 다시 호출한다.
- 헬퍼 함수를 current 변수에 대해 호출해 준다.
- 값을 반환한다.
DFSPreOrder() {
let data = [];
let current = this.root;
function traverse(node) {
data.push(node.value);
if (node.left) traverse(node.left);
if (node.right) traverse(node.right);
}
traverse(current);
return data;
}🟢 후위 순회(Post-Order)
후위 순회는 왼쪽 서브트리, 오른쪽 서브트리, 루트 순서대로 탐색한다. 어떤 노드이든지 모든 자식을 방문한 뒤에 해당 노드를 방문하게 된다.
🟡 의사코드
- 방문했던 노드를 저장하는 변수를 만든다.
- current라 불리는 변수를 만들고, 트리의 루트를 저장해 준다.
- node를 받는 헬퍼 함수를 작성한다.
- 만약 left를 가지고 있는 노드라면, 재귀 방식으로 헬퍼 함수를 다시 호출한다.
- 만약 right를 가지고 있는 노드라면, 재귀 방식으로 헬퍼 함수를 다시 호출한다.
- 방문한 값들을 저장하는 변수에 노드의 값을 push 한다.
- current 변수에 대해 헬퍼 함수를 호출한다.
- 값을 반환한다.
DFSPostOrder() {
let data = [];
let current = this.root;
function traverse(node) {
if(node.left) traverse(node.left);
if(node.right) traverse(node.right);
data.push(node.value)
}
traverse(current);
return data;
}🟢 중위 순회(In-Order)
정위 순회는 왼쪽 서브트리, 루트, 오른쪽 서브트리 순서대로 탐색한다.
🟡 의사코드
- 방문했던 노드를 저장하는 변수를 만든다.
- current라 불리는 변수를 만들고, 트리의 루트를 저장해 준다.
- node를 받는 헬퍼 함수를 작성한다.
- 만약 left를 가지고 있는 노드라면, 재귀 방식으로 헬퍼 함수를 다시 호출한다.
- 방문한 값들을 저장하는 변수에 노드의 값을 push 한다.
- 만약 right를 가지고 있는 노드라면, 재귀 방식으로 헬퍼 함수를 다시 호출한다.
- current 변수에 대해 헬퍼 함수를 호출한다.
- 값을 반환한다.
DFSInOrder() {
let data = [];
let current = this.root;
function traverse(node) {
node.left && traverse(node.left);
data.push(node.value)
node.right && traverse(node.right);
}
traverse(current);
return data;
}🤔 그렇다면 BFS, DFS 뭐가 더 나은가? 어떤 때에 사용하는가?
상황에 따라 장단점이 있다.
우선 너비와 깊이 중에서 어떤 것을 선택해야 할까? 당연히 트리에 따라 다르다.
너 우선 탐색을 큐를 사용한다는 것을 알아두자. 만약 넓은 트리의 경우 큐에 많은 데이터가 들어간다.
즉, 너비가 넓은 트리의 경우 깊이 우선 탐색이 더 적은 공간을 점유한다.
반대로 아주 깊고 긴 트리라면 깊이 우선이 더 많은 공간을 사용할 것이다.
DFS의 전위, 중위, 순위 순회 중 어느 하나 선택해야 선택해야 할 지에 대해 명확한 답은 없다. 중요한 것은 DFS를 사용하냐, BFS를 사용하냐는 것이다.
복습
- 트리는 비선형 데이터 구조로 하나의 루트와 다수의 자식 노드들로 구성되어 있다.
- 이진트리는 아무런 종류의 값을 가질 수 있지만 각 노드는 최대 두 개의 자식을 가질 수 있는 하나의 부모를 가지고 있다.
- 이진 탐색 트리는 이진트리의 특별한 경우(트리가 있고, 그중에 이진트리가 있고, 그중에 이진 탐색 트리가 있는)이다. 이진 탐색 트리는 일종의 순서를 가지는, 정렬된 트리이다. 부모의 왼쪽에 있는 모든 노드는 부모보다 작고 오른쪽에 있는 모든 노드는 크다. 즉, 비교가 가능한 데이터 종류만 사용 가능하다.
- 너비 우선 탐색(BFS)과 깊이 우선 탐색(DFS)으로 트리를 탐색하거나 순회할 수 있다.
'개발자의 공부 > 자료구조&알고리즘' 카테고리의 다른 글
| [자료구조] 해시 테이블(Hash Tables) (0) | 2023.05.11 |
|---|---|
| [자료구조] 힙(Heap) (0) | 2023.04.28 |
| [알고리즘]너비 우선 탐색(BFS, Breadth-First Search) (0) | 2023.03.12 |
| [자료구조]이진 검색 트리(Binary Search Tree) (0) | 2023.03.11 |
| [자료구조]스택(Stack)과 큐(Queue) (0) | 2023.03.05 |
✅ 깊이 우선 탐색(DFS, Depth-First Search)
트리 또는 그래프를 탐색하는 알고리즘으로, 시작점에서 출발하여 가능한 한 깊숙이 탐색해 나가는 방법이다. 이러한 방식으로 트리를 순회할 때, 전위 순회(Pre-Order)는 DFS 중에서도 가장 일반적인 방법 중 하나이며, 전위 순회 외에도 중위 순회(In-Order)나 후위 순회(Post-Order) 등도 DFS의 한 종류이다.

🤔 깊이 우선 탐색의 특징
- 스택이나 재귀 함수를 이용해서 구현 가능하다.
- 탐색 경로를 기억하지 않아, 특정한 경로를 찾는 문제에는 너비 우선 탐색(BFS)이 더 적합하다.
- 구현이 쉽고 속도가 빠르다.
- 한번 방문한 노드를 다시 방문하지 않는 것이 아니기에 무한 그래프에 빠질 위험이 있다. 이를 방지하기 위해 탐색 깊이를 제한하거나, 이미 방문한 노드를 따로 표시해 줘서 재방문하지 않도록 한다.
🟢 전위 순회(Pre-Order)
루트 노드를 가장 먼저 탐색하고, 그다음에 왼쪽 서브트리, 그다음에 오른쪽 서브트리를 탐색한다.
🟡 의사코드
- 방문했던 노드를 저장하는 변수를 만든다.
- current라 불리는 변수를 만들고, 트리의 루트를 저장해 준다. - 시작점
- node를 받는 헬퍼 함수를 작성한다.
- 방문한 값들을 저장하는 변수에 노드의 값을 push 한다.
- 만약 left를 가지고 있는 노드라면, 재귀 방식으로 헬퍼 함수를 다시 호출한다.
- 만약 right를 가지고 있는 노드라면, 재귀 방식으로 헬퍼 함수를 다시 호출한다.
- 헬퍼 함수를 current 변수에 대해 호출해 준다.
- 값을 반환한다.
DFSPreOrder() {
let data = [];
let current = this.root;
function traverse(node) {
data.push(node.value);
if (node.left) traverse(node.left);
if (node.right) traverse(node.right);
}
traverse(current);
return data;
}🟢 후위 순회(Post-Order)
후위 순회는 왼쪽 서브트리, 오른쪽 서브트리, 루트 순서대로 탐색한다. 어떤 노드이든지 모든 자식을 방문한 뒤에 해당 노드를 방문하게 된다.
🟡 의사코드
- 방문했던 노드를 저장하는 변수를 만든다.
- current라 불리는 변수를 만들고, 트리의 루트를 저장해 준다.
- node를 받는 헬퍼 함수를 작성한다.
- 만약 left를 가지고 있는 노드라면, 재귀 방식으로 헬퍼 함수를 다시 호출한다.
- 만약 right를 가지고 있는 노드라면, 재귀 방식으로 헬퍼 함수를 다시 호출한다.
- 방문한 값들을 저장하는 변수에 노드의 값을 push 한다.
- current 변수에 대해 헬퍼 함수를 호출한다.
- 값을 반환한다.
DFSPostOrder() {
let data = [];
let current = this.root;
function traverse(node) {
if(node.left) traverse(node.left);
if(node.right) traverse(node.right);
data.push(node.value)
}
traverse(current);
return data;
}🟢 중위 순회(In-Order)
정위 순회는 왼쪽 서브트리, 루트, 오른쪽 서브트리 순서대로 탐색한다.
🟡 의사코드
- 방문했던 노드를 저장하는 변수를 만든다.
- current라 불리는 변수를 만들고, 트리의 루트를 저장해 준다.
- node를 받는 헬퍼 함수를 작성한다.
- 만약 left를 가지고 있는 노드라면, 재귀 방식으로 헬퍼 함수를 다시 호출한다.
- 방문한 값들을 저장하는 변수에 노드의 값을 push 한다.
- 만약 right를 가지고 있는 노드라면, 재귀 방식으로 헬퍼 함수를 다시 호출한다.
- current 변수에 대해 헬퍼 함수를 호출한다.
- 값을 반환한다.
DFSInOrder() {
let data = [];
let current = this.root;
function traverse(node) {
node.left && traverse(node.left);
data.push(node.value)
node.right && traverse(node.right);
}
traverse(current);
return data;
}🤔 그렇다면 BFS, DFS 뭐가 더 나은가? 어떤 때에 사용하는가?
상황에 따라 장단점이 있다.
우선 너비와 깊이 중에서 어떤 것을 선택해야 할까? 당연히 트리에 따라 다르다.
너 우선 탐색을 큐를 사용한다는 것을 알아두자. 만약 넓은 트리의 경우 큐에 많은 데이터가 들어간다.
즉, 너비가 넓은 트리의 경우 깊이 우선 탐색이 더 적은 공간을 점유한다.
반대로 아주 깊고 긴 트리라면 깊이 우선이 더 많은 공간을 사용할 것이다.
DFS의 전위, 중위, 순위 순회 중 어느 하나 선택해야 선택해야 할 지에 대해 명확한 답은 없다. 중요한 것은 DFS를 사용하냐, BFS를 사용하냐는 것이다.
복습
- 트리는 비선형 데이터 구조로 하나의 루트와 다수의 자식 노드들로 구성되어 있다.
- 이진트리는 아무런 종류의 값을 가질 수 있지만 각 노드는 최대 두 개의 자식을 가질 수 있는 하나의 부모를 가지고 있다.
- 이진 탐색 트리는 이진트리의 특별한 경우(트리가 있고, 그중에 이진트리가 있고, 그중에 이진 탐색 트리가 있는)이다. 이진 탐색 트리는 일종의 순서를 가지는, 정렬된 트리이다. 부모의 왼쪽에 있는 모든 노드는 부모보다 작고 오른쪽에 있는 모든 노드는 크다. 즉, 비교가 가능한 데이터 종류만 사용 가능하다.
- 너비 우선 탐색(BFS)과 깊이 우선 탐색(DFS)으로 트리를 탐색하거나 순회할 수 있다.
'개발자의 공부 > 자료구조&알고리즘' 카테고리의 다른 글
| [자료구조] 해시 테이블(Hash Tables) (0) | 2023.05.11 |
|---|---|
| [자료구조] 힙(Heap) (0) | 2023.04.28 |
| [알고리즘]너비 우선 탐색(BFS, Breadth-First Search) (0) | 2023.03.12 |
| [자료구조]이진 검색 트리(Binary Search Tree) (0) | 2023.03.11 |
| [자료구조]스택(Stack)과 큐(Queue) (0) | 2023.03.05 |
