✅ 그래프(Graphs)란?
객체 간의 관계를 표현하는 데 사용됩니다. 그래프는 노드(node)들과 이들을 연결하는 간선(edge)들의 집합으로 구성된다. 노드는 그래프 안에 있는 개별 요소를 나타내며, 종종 정점(vertex)이라고도 부른다. 노드는 어떤 유형의 데이터나 객체를 담을 수 있으며, 각 노드는 고유한 식별자로 구분된다.
간선(edge)은 노드 사이의 관계를 나타내는 연결선이다. 간선은 노드 간의 관계를 나타내는 데 사용되며, 방향성이 있는 경우도 있고 없는 경우도 있다. 방향성이 없는 그래프에서는 간선이 양방향으로 표현되며, 방향성이 있는 그래프에서는 한 방향으로의 연결만을 나타낸다.
연결 리스트의 경우 노드들이 직선으로 연결되어 있었고, 트리(트리는 그래프의 일종) 같은 경우 한 개의 루트 노드를 가지는 것과 같은 패턴이 있었지만 그래프는 약간 자유로운 형식에 노드가 있고 그 사이에 연결만 있는 것이다.

🟢 그래프 사용 예시
- 소셜 네트워크
- 방향 안내, 위치, 길 찾기 등의 지도 기능
- 라우팅
- Visual hierarchy(시각적 계층 구조)
- 파일 구조 최적화
- 등등
🟢 그래프의 종류
무방향 그래프(undirected graph)
무방향 그래프는 간선에 방향성이 없는 그래프이다. 간선은 단순히 노드 사이의 연결을 나타내며, 양방향으로 이동할 수 있다. 즉, 간선을 통해 노드 A에서 노드 B로 이동할 수 있으면, 노드 B에서 노드 A로도 이동할 수 있다. 이러한 그래프에서는 간선을 통해 노드 간에 관계를 표현할 수 있다. 예를 들어, 소셜 네트워크(페이스북)에서 친구 관계를 나타내는 그래프는 무방향 그래프로 표현할 수 있다.
방향 그래프(directed graph)
방향 그래프는 간선에 방향성이 있는 그래프이다. 간선은 한 방향으로만 이동할 수 있으며, 출발점과 도착점이 있는 방향성을 가지고 있습니다. 따라서, 간선을 통해 노드 A에서 노드 B로 이동할 수 있더라도, 반대 방향인 노드 B에서 노드 A로의 이동은 가능하지 않습니다. 방향 그래프는 의존 관계, 우선순위, 데이터 흐름 등 방향성이 중요한 상황을 모델링하는 데 사용된다. 예를 들어, 웹페이지 간의 링크 구조를 나타내는 그래프는 방향 그래프로 표현될 수 있다. 인스타그램에서의 친구 관계는 방향 그래프를 띤다.
가중치 그래프(weighted graph)
가중치 그래프는 간선에 가중치(weight)라는 추가 정보를 가지고 있는 그래프이다. 간선의 가중치는 노드 사이의 관계의 강도, 거리, 비용 등을 나타낼 수 있다. 가중치 그래프는 네트워크 분석, 최단 경로 찾기, 스케줄링 등에서 활용된다. 예를 들어, 도시 간의 거리를 표현하는 그래프에서 간선의 가중치는 두 도시 간의 거리를 나타낼 수 있다.
비가중치 그래프(unweighted graph)
비가중치 그래프는 모든 간선이 동등한 가중치를 갖는 그래프이다. 간선의 가중치를 고려하지 않고, 그래프의 연결 관계에만 초점을 맞춘다. 비가중치 그래프는 단순한 연결 관계를 모델링하거나 그래프 이론의 기초적인 개념을 이해하는 데 사용된다. 예를 들어, 도시들을 노드로 표현하고 도로를 간선으로 하는 그래프는 비가중치 그래프이다. 모든 도로의 길이나 비용을 동일하게 간주하는 것이다.
그래프를 구현하는 많은 방법과 종류가 있지만 나는 가장 기본적인 두 가지 접근법을 이해하려고 한다.
🔥 인접 행렬(Adjacency Matrix)
그래프는 노드(또는 정점)와 이를 연결하는 간선(또는 에지)으로 구성되며, 인접 행렬은 이러한 노드와 간선의 관계를 행렬로 나타냅니다.
인접 행렬은 다음과 같은 방식으로 정의됩니다:
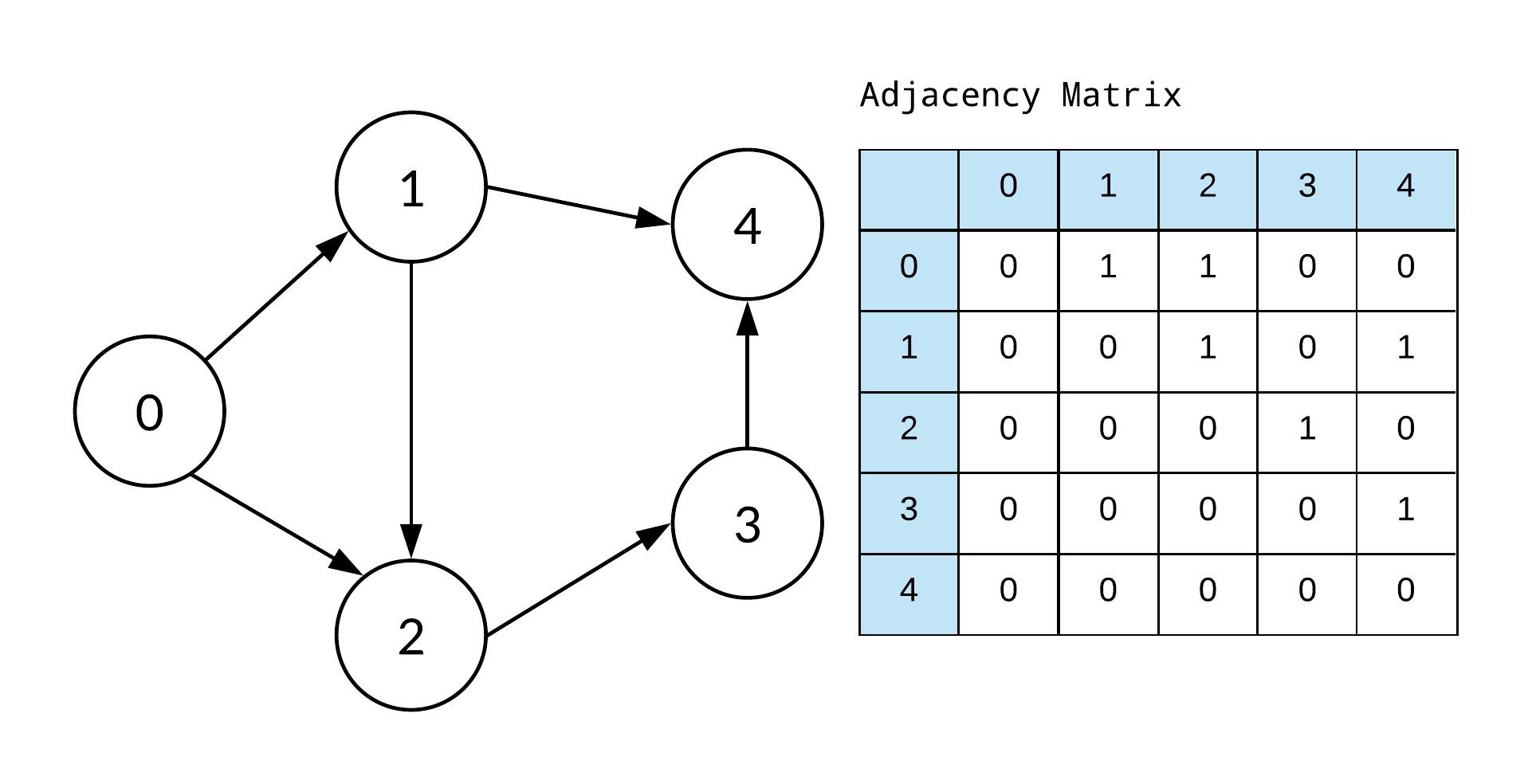
- 노드의 수를 N이라고 하면, N x N 크기의 행렬을 생성한다.
- 행렬의 각 요소 (i, j)는 노드 i와 노드 j 사이의 관계를 나타낸다.
- 만약 노드 i와 노드 j 사이에 간선이 존재한다면, 해당 요소 (i, j)의 값을 1로 설정한다. 이를 통해 인접한 노드 사이의 관계를 표현한다.
- 만약 노드 i와 노드 j 사이에 간선이 존재하지 않는다면, 해당 요소 (i, j)의 값을 0으로 설정한다.
인접 행렬은 가중 그래프(간선에 가중치가 있는 그래프)의 경우에도 사용할 수 있으며, 간선의 가중치를 해당 요소에 저장할 수 있다. 무방향 그래프의 경우 인접 행렬은 대칭 행렬이 된다.
그래프의 구조를 효과적으로 나타낼 수 있으며, 그래프 알고리즘 및 연산을 수행할 때 유용하게 사용된다. 그래프의 크기가 작을 때나 밀집된 그래프에 적합한 표현 방법이며 그래프가 희소하거나 큰 경우, 인접 리스트와 같은 다른 표현 방법이 메모리를 더 효율적으로 사용할 수 있다.
🔥 인접 리스트 (Adjacency List)
- 노드의 수를 N이라고 하면, N개의 리스트(또는 배열)를 생성한다. 각 리스트는 각각의 노드에 대응한다.
- 각 리스트에는 해당 노드와 인접한 다른 노드들을 나타내는 요소들을 저장한다. 이 요소들은 해당 노드와 직접적으로 연결된 노드들을 나타낸다.
- 방향 그래프의 경우, 각 노드의 인접 리스트에는 해당 노드에서 다른 노드로 나가는 간선만 저장되고 양방향 그래프의 경우, 두 노드 사이의 간선은 두 노드의 인접 리스트에 모두 저장된다.
- 추가적인 정보를 저장하기 위해 간선의 가중치 또는 다른 속성을 함께 저장할 수 있다.
인접 리스트는 희소 그래프(간선의 수가 상대적으로 적은 그래프)를 효과적으로 표현할 수 있으며, 메모리를 효율적으로 사용할 수 있고 그래프의 크기가 크거나 동적으로 변하는 경우에도 유용하다. 그래프 탐색 알고리즘(예: 깊이 우선 탐색, 너비 우선 탐색) 및 다양한 그래프 기반 문제를 해결할 때 인접 리스트가 종종 사용된다.

Runtime Analysis
Below is a chart of the most common graph operations and their runtimes for each of the graph representations. In the chart below, V(정점의 개수) represents the number of verticies in the graph and E(간선의 수) represents the number of edges in the graph.
| Representation | Getting all adjacent edges for a vertex | Traversing entire graph | hasEdge(u, v) | Space |
| Adjacency matrix | O(V) | O(V^2) | O(1) | O(V^2) |
| Edge Set | O(E) | O(E) | O(E) | O(E) |
| Adjacency List | O(1) | O(V + E) | O(max number of edges a vertex has) | O(E + V) |
출처: https://guides.codepath.com/compsci/Graphs
Representation (표현 방법)
- Adjacency matrix (인접 행렬): 그래프를 인접 행렬로 표현할 때, 모든 노드 쌍 간의 연결 여부를 상수 시간 O(1)에 확인할 수 있다. 그러나 공간 복잡도는 O(V^2)로 노드의 수에 제곱 비례한다.
- Edge Set (간선 집합): 그래프를 간선의 집합으로 표현할 때, 간선을 확인하는 데는 해당 간선 집합을 순회해야 하므로 O(E)의 시간이 걸린다. 공간 복잡도는 O(E)로 간선의 수에 비례한다.
- Adjacency List (인접 리스트): 그래프를 인접 리스트로 표현할 때, 각 노드에 대한 인접한 노드들을 확인하는 데 상수 시간 O(1)이 걸린다. 그래프를 전체적으로 순회할 때는 노드의 수와 간선의 수에 비례하는 시간이 걸리며, 공간 복잡도는 O(E + V)이다.
Getting all adjacent edges for a vertex (특정 노드에 인접한 간선 모두 가져오기)
- Adjacency matrix: 특정 노드의 인접한 간선을 모두 가져오려면 해당 노드의 행을 검색해야 하므로 O(V).
- Edge Set: 특정 노드에 인접한 간선을 찾으려면 간선 집합을 순회해야 하므로 O(E).
- Adjacency List: 특정 노드의 인접한 간선을 모두 가져오려면 해당 노드의 인접 리스트를 조회하면 되므로 O(1).
Traversing entire graph (전체 그래프 순회)
- Adjacency matrix: 전체 그래프를 순회할 때 모든 노드 쌍을 확인해야 하므로 O(V^2).
- Edge Set: 전체 간선 집합을 순회하면 되므로 O(E).
- Adjacency List: 전체 그래프를 순회할 때 노드의 수와 간선의 수에 비례하는 시간이 걸린다 O(V + E).
hasEdge(u, v) (간선 확인)
- Adjacency matrix: 두 노드 간의 연결 여부를 상수 시간 O(1)에 확인할 수 있다.
- Edge Set: 두 노드 사이의 간선을 찾기 위해서 간선 집합을 순회해야 하므로 O(E).
- Adjacency List: 두 노드 사이의 간선을 확인하는 데 O(max number of edges a vertex has) 시간이 걸린다.
Space (저장 공간)
- Adjacency matrix: 저장 공간은 노드의 수에 제곱 비례하여 O(V^2).
- Edge Set: 저장 공간은 간선의 수에 비례하여 O(E).
- Adjacency List: 저장 공간은 노드와 간선의 수에 비례하여 O(E + V).
| Operation | Adjacency List | Adjacency Matrix |
| Add Vertex | O(1) | O(|V^2|) |
| Add Edge | O(1) | O(1) |
| Remove Vertex | O(|V| + |E|) | O(|V^2|) |
| Remove Edge | O(|E|) | O(1) |
| Query | O(|V| + |E|) | O(1) |
Add Vertex (노드 추가)
- 인접 리스트: 노드를 추가할 때는 단순히 새로운 노드를 나타내는 리스트를 생성하면 되므로 O(1).
- 인접 행렬: 노드 추가 시, 새로운 행과 열을 추가해야 하므로 행렬의 크기에 따라 시간이 O(|V^2|).
Add Edge (간선 추가)
- 인접 리스트: 두 노드를 연결하는 간선을 추가할 때 O(1).
- 인접 행렬: 간선을 추가하는 데도 O(1).
Remove Vertex (노드 제거)
- 인접 리스트: 노드를 제거할 때 해당 노드와 관련된 간선들을 모두 제거해야 하므로 O(|V| + |E|).
- 인접 행렬: 노드를 제거할 때 관련된 행과 열을 모두 제거해야 하므로 O(|V^2|).
Remove Edge (간선 제거)
- 인접 리스트: 간선을 제거할 때 해당 간선을 포함하는 노드의 인접 리스트에서 제거하므로 O(|E|).
- 인접 행렬: 간선을 제거할 때도 O(1).
Query (조회)
- 인접 리스트: 두 노드가 연결되어 있는지 확인하려면 해당 노드의 인접 리스트를 조회해야 하므로 O(|V| + |E|).
- 인접 행렬: 두 노드가 연결되어 있는지 확인하는 데 O(1).
Adjacency List VS Adjacency Matrix
인접 리스트: 더 적은 공간을 차지함(희소 그래프에서), 모든 Edge에서 더 빠르게 반복 가능, 특정 Edge를 조회하는 속도가 느릴 수 있음.
인접행렬: 공간을 더 많이 차지함(희소 그래프에서), 모든 Edge에서 반복 속도가 느림, 특정 Edge를 조회하는 속도가 빠름.
*희소 그래프 - 그래프에서 간선의 수가 상대적으로 적은 경우
✅ 인접 리스트 작성해 보기
기본 골격
class Graph {
constructor() {
this.adjacencyList = {}
}
}
1. Adding a vertex
- addVertex 메서드는 vertex의 이름을 받는다. vertex의 이름과 함께 인접 리스트에 키를 추가하고 그 값을 빈 배열로 설정한다.
addVertex(vertex) {
if(!this.adjacencyList[vertex]) this.adjacencyList[vertex] = [];
}
2. Adding an edge
- 두 vertex를 받고, vertex1의 key를 vertex2의 배열에 푸시, vertex2의 key를 vertex1의 배열에 푸시한다. 에러와 유효하지 않은 vertex에 대한 핸들링은 신경 쓰지 않는다.
addEdge(v1, v2) {
this.adjacencyList[v1].push(v2)
this.adjacencyList[v2].push(v1)
}
3. Removing an edge
- 두 vertex를 받고, vertex1의 키를 vertex2를 포함하지 않는 배열로 재할당, vertex2의 키를 vertex1을 포함하지 않는 배열로 재할당한다.
removeEdge(v1, v2) {
this.adjacencyList[v1] = this.adjacencyList[v1].filter(
v => v !== v2
);
this.adjacencyList[v2] = this.adjacencyList[v2].filter(
v => v !== v1
);
}
4. Removing a vertex
- 제거할 vertex를 받고, 해당하는 vertex뿐만 아니라 다른 vertex 또한 loop 하면서, 해당 loop안에서 removeEdge를 호출하여 다른 vertex내에 있는 값들을 삭제하고 해당 vertex의 key를 삭제한다.
removeVertex(vertex) {
while (this.adjacencyList[vertex].length) {
const adjacentVertex = this.adjacencyList[vertex].pop()
this.removeEdge(vertex, adjacentVertex)
}
delete this.adjacencyList[vertex]
}아주 간단하게 그래프의 구현에 대해서 알아봤다. 조금 더 깊게 알아보자.
✅ 그래프 순회(Graph Traversal)
순회라고 하면 방문, 최신화, 확인, 탐색, 출력 등을 그래프의 모든 정점에 대해 수행하는 것이다.
그래프 순회의 목적
- 그래프의 연결 여부 확인: 그래프가 연결되어 있는지 확인하거나, 연결 요소를 찾는 데 사용됨.
- 경로 찾기: 두 정점 사이의 경로를 찾는 데 사용됨.
- 사이클 검출: 그래프 내에 순환 경로가 있는지 검사하는 데 사용됨.
- 위상 정렬: 방향 그래프의 정점들을 순서대로 나열하는 데 사용됨.
깊이 우선 순회(DFS)
한 노드에서 시작하여 가능한 한 깊숙이 들어가서 더 이상 진행할 수 없을 때 다시 후진하며 그래프를 순회한다.
🟡 재귀적 용법
의사코드
- 시작점인 노드를 받는 함수를 작성한다.
- 결과를 저장하고, 마지막에 반환할 result 변수를 만든다.
- 방문한 vertices를 저장할 객체를 만든다.
- vertex를 받는 helper 함수를 작성한다.
- vertex가 비어있으면 return 한다.
- result 배열에 vertex를 push 하고, 방문 기록 객체에 해당 vertex를 넣는다.
- vertex의 모든 인접점에 대해 loop를 수행하고, 만약 방문하지 않았다면 해당 정점에 대해 헬퍼 함수를 재귀 방식으로 호출한다.
- 시작 vertex로 해당 helper 함수를 호출한다.
depthFirstRecursive(start) {
const result = [];
const visited = {};
const adjacencyList = this.adjacencyList;
(function dfs(vertex){
if(!vertex) return null;
visited[vertex] = true;
result.push(vertex);
adjacencyList[vertex].forEach(neighbor => {
if(!visited[neighbor]) {
return dfs(neighbor)
}
})
}) (start)
return result
}🟡 반복적 용법
의사코드
- 노드를 받는 함수를 만들고, 정접들을 추적할 stack을 생성한다. (배열 혹은 리스트)
- 최종 결과를 저장할 배열이나 리스트를 만든다.
- 방문한 vertex들을 마킹할 빈 객체도 만들어 준다.
- 시작하는 지점의 vertex를 스택에 넣어주고, 방문 표시를 해준다.
- stack에서 while loop를 실행한다.
- 다음 vertex를 stack으로부터 pop 한다.
- 만약 해당 정점을 아직 방문하지 않았다면
- 방문 표시를 해주고, result에 추가한 다음, 그 인접점들을 모두 stack에 push 한다.
- result를 반환한다.
depthFirstIterative(start) {
const stack = [start];
const result = [];
const visited = {};
let currentVertex;
visited[start] = true;
while(stack.length) {
console.log(stack)
currentVertex = stack.pop();
result.push(currentVertex);
this.adjacencyList[currentVertex].forEach(neighbor => {
if(!visited[neighbor]) {
visited[neighbor] = true;
stack.push(neighbor);
}
})
}
return result;
}
너비 우선 순회(BFS)
한 노드에서 시작하여 인접한 모든 노드를 우선 방문한 다음, 그 노드들의 인접한 노드를 순차적으로 방문하는 방식으로 그래프를 순회한다.
의사 코드
- 시작 vertex를 받는 함수는 만든다.
- queue를 만들고 시작 vertex를 넣어준다.
- 최종 결과를 저장할 배열과 방문한 node들을 마킹할 빈 객체를 만든다.
- 시작 vertex를 마킹한다.
- while loop를 이용해 queue에 무언가가 들어있는 한
- queue에서 첫 번째 vertex를 제거하고, 결과를 저장하고 있는 배열에 push 해준다.
- 각 vertex에 있는 각 인접점에 대해 아직 방문하지 않았다면 방문한 것으로 표시하고 큐에 추가해 준 다음에 push를 해준다.
breathFirst(start) {
const queue = [start];
const result = [];
const visited = {};
let currentVertex
visited[start] = true;
while(queue.length) {
currentVertex = queue.shift();
result.push(currentVertex)
this.adjacencyList[currentVertex].forEach(neightbor => {
if(!visited[neightbor]) {
visited[neightbor] = true;
queue.push(neightbor)
}
})
}
return result;
}'개발자의 공부 > 자료구조&알고리즘' 카테고리의 다른 글
| 다익스트라 알고리즘(Dijkstra's Algorithm) (0) | 2023.10.05 |
|---|---|
| [자료구조] 해시 테이블(Hash Tables) (0) | 2023.05.11 |
| [자료구조] 힙(Heap) (0) | 2023.04.28 |
| [알고리즘]깊이 우선 탐색(DFS, Depth-First Search) (0) | 2023.03.16 |
| [알고리즘]너비 우선 탐색(BFS, Breadth-First Search) (0) | 2023.03.12 |
✅ 그래프(Graphs)란?
객체 간의 관계를 표현하는 데 사용됩니다. 그래프는 노드(node)들과 이들을 연결하는 간선(edge)들의 집합으로 구성된다. 노드는 그래프 안에 있는 개별 요소를 나타내며, 종종 정점(vertex)이라고도 부른다. 노드는 어떤 유형의 데이터나 객체를 담을 수 있으며, 각 노드는 고유한 식별자로 구분된다.
간선(edge)은 노드 사이의 관계를 나타내는 연결선이다. 간선은 노드 간의 관계를 나타내는 데 사용되며, 방향성이 있는 경우도 있고 없는 경우도 있다. 방향성이 없는 그래프에서는 간선이 양방향으로 표현되며, 방향성이 있는 그래프에서는 한 방향으로의 연결만을 나타낸다.
연결 리스트의 경우 노드들이 직선으로 연결되어 있었고, 트리(트리는 그래프의 일종) 같은 경우 한 개의 루트 노드를 가지는 것과 같은 패턴이 있었지만 그래프는 약간 자유로운 형식에 노드가 있고 그 사이에 연결만 있는 것이다.

🟢 그래프 사용 예시
- 소셜 네트워크
- 방향 안내, 위치, 길 찾기 등의 지도 기능
- 라우팅
- Visual hierarchy(시각적 계층 구조)
- 파일 구조 최적화
- 등등
🟢 그래프의 종류
무방향 그래프(undirected graph)
무방향 그래프는 간선에 방향성이 없는 그래프이다. 간선은 단순히 노드 사이의 연결을 나타내며, 양방향으로 이동할 수 있다. 즉, 간선을 통해 노드 A에서 노드 B로 이동할 수 있으면, 노드 B에서 노드 A로도 이동할 수 있다. 이러한 그래프에서는 간선을 통해 노드 간에 관계를 표현할 수 있다. 예를 들어, 소셜 네트워크(페이스북)에서 친구 관계를 나타내는 그래프는 무방향 그래프로 표현할 수 있다.
방향 그래프(directed graph)
방향 그래프는 간선에 방향성이 있는 그래프이다. 간선은 한 방향으로만 이동할 수 있으며, 출발점과 도착점이 있는 방향성을 가지고 있습니다. 따라서, 간선을 통해 노드 A에서 노드 B로 이동할 수 있더라도, 반대 방향인 노드 B에서 노드 A로의 이동은 가능하지 않습니다. 방향 그래프는 의존 관계, 우선순위, 데이터 흐름 등 방향성이 중요한 상황을 모델링하는 데 사용된다. 예를 들어, 웹페이지 간의 링크 구조를 나타내는 그래프는 방향 그래프로 표현될 수 있다. 인스타그램에서의 친구 관계는 방향 그래프를 띤다.
가중치 그래프(weighted graph)
가중치 그래프는 간선에 가중치(weight)라는 추가 정보를 가지고 있는 그래프이다. 간선의 가중치는 노드 사이의 관계의 강도, 거리, 비용 등을 나타낼 수 있다. 가중치 그래프는 네트워크 분석, 최단 경로 찾기, 스케줄링 등에서 활용된다. 예를 들어, 도시 간의 거리를 표현하는 그래프에서 간선의 가중치는 두 도시 간의 거리를 나타낼 수 있다.
비가중치 그래프(unweighted graph)
비가중치 그래프는 모든 간선이 동등한 가중치를 갖는 그래프이다. 간선의 가중치를 고려하지 않고, 그래프의 연결 관계에만 초점을 맞춘다. 비가중치 그래프는 단순한 연결 관계를 모델링하거나 그래프 이론의 기초적인 개념을 이해하는 데 사용된다. 예를 들어, 도시들을 노드로 표현하고 도로를 간선으로 하는 그래프는 비가중치 그래프이다. 모든 도로의 길이나 비용을 동일하게 간주하는 것이다.
그래프를 구현하는 많은 방법과 종류가 있지만 나는 가장 기본적인 두 가지 접근법을 이해하려고 한다.
🔥 인접 행렬(Adjacency Matrix)
그래프는 노드(또는 정점)와 이를 연결하는 간선(또는 에지)으로 구성되며, 인접 행렬은 이러한 노드와 간선의 관계를 행렬로 나타냅니다.
인접 행렬은 다음과 같은 방식으로 정의됩니다:
- 노드의 수를 N이라고 하면, N x N 크기의 행렬을 생성한다.
- 행렬의 각 요소 (i, j)는 노드 i와 노드 j 사이의 관계를 나타낸다.
- 만약 노드 i와 노드 j 사이에 간선이 존재한다면, 해당 요소 (i, j)의 값을 1로 설정한다. 이를 통해 인접한 노드 사이의 관계를 표현한다.
- 만약 노드 i와 노드 j 사이에 간선이 존재하지 않는다면, 해당 요소 (i, j)의 값을 0으로 설정한다.
인접 행렬은 가중 그래프(간선에 가중치가 있는 그래프)의 경우에도 사용할 수 있으며, 간선의 가중치를 해당 요소에 저장할 수 있다. 무방향 그래프의 경우 인접 행렬은 대칭 행렬이 된다.
그래프의 구조를 효과적으로 나타낼 수 있으며, 그래프 알고리즘 및 연산을 수행할 때 유용하게 사용된다. 그래프의 크기가 작을 때나 밀집된 그래프에 적합한 표현 방법이며 그래프가 희소하거나 큰 경우, 인접 리스트와 같은 다른 표현 방법이 메모리를 더 효율적으로 사용할 수 있다.

🔥 인접 리스트 (Adjacency List)
- 노드의 수를 N이라고 하면, N개의 리스트(또는 배열)를 생성한다. 각 리스트는 각각의 노드에 대응한다.
- 각 리스트에는 해당 노드와 인접한 다른 노드들을 나타내는 요소들을 저장한다. 이 요소들은 해당 노드와 직접적으로 연결된 노드들을 나타낸다.
- 방향 그래프의 경우, 각 노드의 인접 리스트에는 해당 노드에서 다른 노드로 나가는 간선만 저장되고 양방향 그래프의 경우, 두 노드 사이의 간선은 두 노드의 인접 리스트에 모두 저장된다.
- 추가적인 정보를 저장하기 위해 간선의 가중치 또는 다른 속성을 함께 저장할 수 있다.
인접 리스트는 희소 그래프(간선의 수가 상대적으로 적은 그래프)를 효과적으로 표현할 수 있으며, 메모리를 효율적으로 사용할 수 있고 그래프의 크기가 크거나 동적으로 변하는 경우에도 유용하다. 그래프 탐색 알고리즘(예: 깊이 우선 탐색, 너비 우선 탐색) 및 다양한 그래프 기반 문제를 해결할 때 인접 리스트가 종종 사용된다.

Runtime Analysis
Below is a chart of the most common graph operations and their runtimes for each of the graph representations. In the chart below, V(정점의 개수) represents the number of verticies in the graph and E(간선의 수) represents the number of edges in the graph.
| Representation | Getting all adjacent edges for a vertex | Traversing entire graph | hasEdge(u, v) | Space |
| Adjacency matrix | O(V) | O(V^2) | O(1) | O(V^2) |
| Edge Set | O(E) | O(E) | O(E) | O(E) |
| Adjacency List | O(1) | O(V + E) | O(max number of edges a vertex has) | O(E + V) |
출처: https://guides.codepath.com/compsci/Graphs
Representation (표현 방법)
- Adjacency matrix (인접 행렬): 그래프를 인접 행렬로 표현할 때, 모든 노드 쌍 간의 연결 여부를 상수 시간 O(1)에 확인할 수 있다. 그러나 공간 복잡도는 O(V^2)로 노드의 수에 제곱 비례한다.
- Edge Set (간선 집합): 그래프를 간선의 집합으로 표현할 때, 간선을 확인하는 데는 해당 간선 집합을 순회해야 하므로 O(E)의 시간이 걸린다. 공간 복잡도는 O(E)로 간선의 수에 비례한다.
- Adjacency List (인접 리스트): 그래프를 인접 리스트로 표현할 때, 각 노드에 대한 인접한 노드들을 확인하는 데 상수 시간 O(1)이 걸린다. 그래프를 전체적으로 순회할 때는 노드의 수와 간선의 수에 비례하는 시간이 걸리며, 공간 복잡도는 O(E + V)이다.
Getting all adjacent edges for a vertex (특정 노드에 인접한 간선 모두 가져오기)
- Adjacency matrix: 특정 노드의 인접한 간선을 모두 가져오려면 해당 노드의 행을 검색해야 하므로 O(V).
- Edge Set: 특정 노드에 인접한 간선을 찾으려면 간선 집합을 순회해야 하므로 O(E).
- Adjacency List: 특정 노드의 인접한 간선을 모두 가져오려면 해당 노드의 인접 리스트를 조회하면 되므로 O(1).
Traversing entire graph (전체 그래프 순회)
- Adjacency matrix: 전체 그래프를 순회할 때 모든 노드 쌍을 확인해야 하므로 O(V^2).
- Edge Set: 전체 간선 집합을 순회하면 되므로 O(E).
- Adjacency List: 전체 그래프를 순회할 때 노드의 수와 간선의 수에 비례하는 시간이 걸린다 O(V + E).
hasEdge(u, v) (간선 확인)
- Adjacency matrix: 두 노드 간의 연결 여부를 상수 시간 O(1)에 확인할 수 있다.
- Edge Set: 두 노드 사이의 간선을 찾기 위해서 간선 집합을 순회해야 하므로 O(E).
- Adjacency List: 두 노드 사이의 간선을 확인하는 데 O(max number of edges a vertex has) 시간이 걸린다.
Space (저장 공간)
- Adjacency matrix: 저장 공간은 노드의 수에 제곱 비례하여 O(V^2).
- Edge Set: 저장 공간은 간선의 수에 비례하여 O(E).
- Adjacency List: 저장 공간은 노드와 간선의 수에 비례하여 O(E + V).
| Operation | Adjacency List | Adjacency Matrix |
| Add Vertex | O(1) | O(|V^2|) |
| Add Edge | O(1) | O(1) |
| Remove Vertex | O(|V| + |E|) | O(|V^2|) |
| Remove Edge | O(|E|) | O(1) |
| Query | O(|V| + |E|) | O(1) |
Add Vertex (노드 추가)
- 인접 리스트: 노드를 추가할 때는 단순히 새로운 노드를 나타내는 리스트를 생성하면 되므로 O(1).
- 인접 행렬: 노드 추가 시, 새로운 행과 열을 추가해야 하므로 행렬의 크기에 따라 시간이 O(|V^2|).
Add Edge (간선 추가)
- 인접 리스트: 두 노드를 연결하는 간선을 추가할 때 O(1).
- 인접 행렬: 간선을 추가하는 데도 O(1).
Remove Vertex (노드 제거)
- 인접 리스트: 노드를 제거할 때 해당 노드와 관련된 간선들을 모두 제거해야 하므로 O(|V| + |E|).
- 인접 행렬: 노드를 제거할 때 관련된 행과 열을 모두 제거해야 하므로 O(|V^2|).
Remove Edge (간선 제거)
- 인접 리스트: 간선을 제거할 때 해당 간선을 포함하는 노드의 인접 리스트에서 제거하므로 O(|E|).
- 인접 행렬: 간선을 제거할 때도 O(1).
Query (조회)
- 인접 리스트: 두 노드가 연결되어 있는지 확인하려면 해당 노드의 인접 리스트를 조회해야 하므로 O(|V| + |E|).
- 인접 행렬: 두 노드가 연결되어 있는지 확인하는 데 O(1).
Adjacency List VS Adjacency Matrix
인접 리스트: 더 적은 공간을 차지함(희소 그래프에서), 모든 Edge에서 더 빠르게 반복 가능, 특정 Edge를 조회하는 속도가 느릴 수 있음.
인접행렬: 공간을 더 많이 차지함(희소 그래프에서), 모든 Edge에서 반복 속도가 느림, 특정 Edge를 조회하는 속도가 빠름.
*희소 그래프 - 그래프에서 간선의 수가 상대적으로 적은 경우
✅ 인접 리스트 작성해 보기
기본 골격
class Graph {
constructor() {
this.adjacencyList = {}
}
}
1. Adding a vertex
- addVertex 메서드는 vertex의 이름을 받는다. vertex의 이름과 함께 인접 리스트에 키를 추가하고 그 값을 빈 배열로 설정한다.
addVertex(vertex) {
if(!this.adjacencyList[vertex]) this.adjacencyList[vertex] = [];
}
2. Adding an edge
- 두 vertex를 받고, vertex1의 key를 vertex2의 배열에 푸시, vertex2의 key를 vertex1의 배열에 푸시한다. 에러와 유효하지 않은 vertex에 대한 핸들링은 신경 쓰지 않는다.
addEdge(v1, v2) {
this.adjacencyList[v1].push(v2)
this.adjacencyList[v2].push(v1)
}
3. Removing an edge
- 두 vertex를 받고, vertex1의 키를 vertex2를 포함하지 않는 배열로 재할당, vertex2의 키를 vertex1을 포함하지 않는 배열로 재할당한다.
removeEdge(v1, v2) {
this.adjacencyList[v1] = this.adjacencyList[v1].filter(
v => v !== v2
);
this.adjacencyList[v2] = this.adjacencyList[v2].filter(
v => v !== v1
);
}
4. Removing a vertex
- 제거할 vertex를 받고, 해당하는 vertex뿐만 아니라 다른 vertex 또한 loop 하면서, 해당 loop안에서 removeEdge를 호출하여 다른 vertex내에 있는 값들을 삭제하고 해당 vertex의 key를 삭제한다.
removeVertex(vertex) {
while (this.adjacencyList[vertex].length) {
const adjacentVertex = this.adjacencyList[vertex].pop()
this.removeEdge(vertex, adjacentVertex)
}
delete this.adjacencyList[vertex]
}아주 간단하게 그래프의 구현에 대해서 알아봤다. 조금 더 깊게 알아보자.
✅ 그래프 순회(Graph Traversal)
순회라고 하면 방문, 최신화, 확인, 탐색, 출력 등을 그래프의 모든 정점에 대해 수행하는 것이다.
그래프 순회의 목적
- 그래프의 연결 여부 확인: 그래프가 연결되어 있는지 확인하거나, 연결 요소를 찾는 데 사용됨.
- 경로 찾기: 두 정점 사이의 경로를 찾는 데 사용됨.
- 사이클 검출: 그래프 내에 순환 경로가 있는지 검사하는 데 사용됨.
- 위상 정렬: 방향 그래프의 정점들을 순서대로 나열하는 데 사용됨.
깊이 우선 순회(DFS)
한 노드에서 시작하여 가능한 한 깊숙이 들어가서 더 이상 진행할 수 없을 때 다시 후진하며 그래프를 순회한다.
🟡 재귀적 용법
의사코드
- 시작점인 노드를 받는 함수를 작성한다.
- 결과를 저장하고, 마지막에 반환할 result 변수를 만든다.
- 방문한 vertices를 저장할 객체를 만든다.
- vertex를 받는 helper 함수를 작성한다.
- vertex가 비어있으면 return 한다.
- result 배열에 vertex를 push 하고, 방문 기록 객체에 해당 vertex를 넣는다.
- vertex의 모든 인접점에 대해 loop를 수행하고, 만약 방문하지 않았다면 해당 정점에 대해 헬퍼 함수를 재귀 방식으로 호출한다.
- 시작 vertex로 해당 helper 함수를 호출한다.
depthFirstRecursive(start) {
const result = [];
const visited = {};
const adjacencyList = this.adjacencyList;
(function dfs(vertex){
if(!vertex) return null;
visited[vertex] = true;
result.push(vertex);
adjacencyList[vertex].forEach(neighbor => {
if(!visited[neighbor]) {
return dfs(neighbor)
}
})
}) (start)
return result
}🟡 반복적 용법
의사코드
- 노드를 받는 함수를 만들고, 정접들을 추적할 stack을 생성한다. (배열 혹은 리스트)
- 최종 결과를 저장할 배열이나 리스트를 만든다.
- 방문한 vertex들을 마킹할 빈 객체도 만들어 준다.
- 시작하는 지점의 vertex를 스택에 넣어주고, 방문 표시를 해준다.
- stack에서 while loop를 실행한다.
- 다음 vertex를 stack으로부터 pop 한다.
- 만약 해당 정점을 아직 방문하지 않았다면
- 방문 표시를 해주고, result에 추가한 다음, 그 인접점들을 모두 stack에 push 한다.
- result를 반환한다.
depthFirstIterative(start) {
const stack = [start];
const result = [];
const visited = {};
let currentVertex;
visited[start] = true;
while(stack.length) {
console.log(stack)
currentVertex = stack.pop();
result.push(currentVertex);
this.adjacencyList[currentVertex].forEach(neighbor => {
if(!visited[neighbor]) {
visited[neighbor] = true;
stack.push(neighbor);
}
})
}
return result;
}
너비 우선 순회(BFS)
한 노드에서 시작하여 인접한 모든 노드를 우선 방문한 다음, 그 노드들의 인접한 노드를 순차적으로 방문하는 방식으로 그래프를 순회한다.
의사 코드
- 시작 vertex를 받는 함수는 만든다.
- queue를 만들고 시작 vertex를 넣어준다.
- 최종 결과를 저장할 배열과 방문한 node들을 마킹할 빈 객체를 만든다.
- 시작 vertex를 마킹한다.
- while loop를 이용해 queue에 무언가가 들어있는 한
- queue에서 첫 번째 vertex를 제거하고, 결과를 저장하고 있는 배열에 push 해준다.
- 각 vertex에 있는 각 인접점에 대해 아직 방문하지 않았다면 방문한 것으로 표시하고 큐에 추가해 준 다음에 push를 해준다.
breathFirst(start) {
const queue = [start];
const result = [];
const visited = {};
let currentVertex
visited[start] = true;
while(queue.length) {
currentVertex = queue.shift();
result.push(currentVertex)
this.adjacencyList[currentVertex].forEach(neightbor => {
if(!visited[neightbor]) {
visited[neightbor] = true;
queue.push(neightbor)
}
})
}
return result;
}'개발자의 공부 > 자료구조&알고리즘' 카테고리의 다른 글
| 다익스트라 알고리즘(Dijkstra's Algorithm) (0) | 2023.10.05 |
|---|---|
| [자료구조] 해시 테이블(Hash Tables) (0) | 2023.05.11 |
| [자료구조] 힙(Heap) (0) | 2023.04.28 |
| [알고리즘]깊이 우선 탐색(DFS, Depth-First Search) (0) | 2023.03.16 |
| [알고리즘]너비 우선 탐색(BFS, Breadth-First Search) (0) | 2023.03.12 |
